Hg's Blog

学习 分享 进步

0%

注意力机制

发表于 更新于

注意力机制

什么是注意力机制

在深度学习领域，模型往往需要接收和处理大量的数据，然而在特定的某个时刻，往往只有少部分的某些数据是重要的

心理学框架：人类根据随意线索和不随意线索选择注意点

卷积、全连接、池化层都只考虑不随意线索（将本身容易抽取的特征抽取出来）

注意力机制则考虑随意线索

  • 随意线索对应查询（query）
  • 每个输入是值（value）和不随意线索（key）的对
  • 通过注意力池化层来有偏向性地选择某些输入

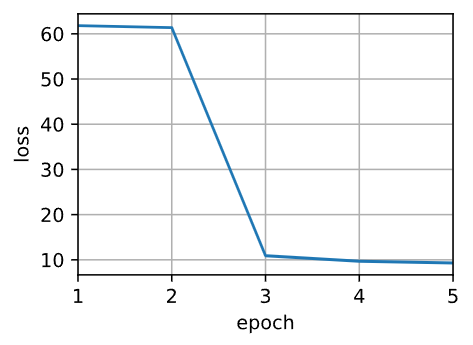
非参注意力池化层

对于给定的数据$(x_i,y_i),i=1,…,n$）（key, value）

最简单的方案：平均池化 $f(x)=\frac{1}{n}\sum\limits_{i}{y_i}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import matplotlib.pyplot as plt
import torch
from torch import nn
from d2l import torch as d2l

n_train = 50
# torch.rand()产生一个服从均匀分布的张量，张量内的数据包含从区间[0,1)的随机数。
# 参数size是一个整数序列，用于定义张量大小
# torch.sort()返回两个值 第一个为排序后的张量，第二个为原来的索引
x_train, _ = torch.sort(torch.rand(n_train) * 5)   # *5表示将[0,1)扩展到[0,5)

def f(x):   # 真实的f(x)  需要被拟合
  return 2 * torch.cos(x) + x ** 0.7

y_train = f(x_train) + torch.normal(0, 0.5, (n_train,))
# 测试集
x_test = torch.arange(0, 5, 0.1)
y_truth = f(x_test)
n_test = len(x_test)

def plot_kernel_reg(y_hat):
  d2l.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'pred'], xlim=[0, 5], ylim=[-1, 5])
  d2l.plt.plot(x_train, y_train, 'o', alpha=0.5)
  plt.show()

y_hat = torch.repeat_interleave(y_train.mean(), n_test)
plot_kernel_reg(y_hat)

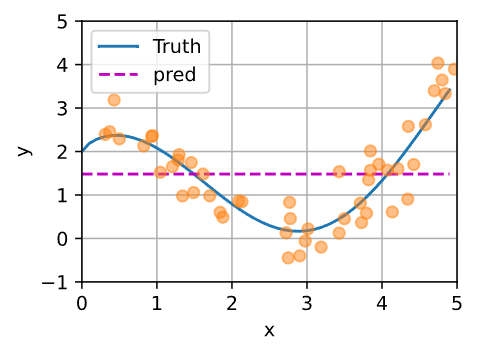
image-20220802055649966

更好的方案：Nadaraya-Watson 核回归：

（找到离已知值最近的值，类似于KNN）

1
2
3
4
5
6
7
8
9
#X_repeat的形状为(n_test, n_train) 同一行的所有元素（测试输入，查询）都相同 每一行的结果为一个点
X_repeat = x_test.repeat_interleave(n_train).reshape((-1, n_train))  #重复n_train次
# x_train包含着键。attention_weights的形状：(n_test,n_train)
# 每一行都包含着要在给定的每个查询的值（y_train）之间分配的注意力权重
attention_weights = nn.functional.softmax(-(X_repeat - x_train) ** 2 / 2, dim=1)
# y_hat的每个元素都是值的加权平均值，其中的权重是注意力权重
# y_train = y_train.reshape(-1, 1)  #这一步可以不用做 matmul可以实现不同维度的矩阵成绩 但如果使用mm函数进行矩阵乘积必须转化为一列
y_hat = torch.matmul(attention_weights, y_train)
plot_kernel_reg(y_hat)

image-20220802055728239

参数化注意力机制

在此基础上引入可学习的参数w

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class NWKernelRegression(nn.Module):
  def __init__(self, **kwargs):
    super(NWKernelRegression, self).__init__()
    self.w = nn.Parameter(torch.rand((1, ), requires_grad=True))

  def forward(self, queries, keys, values):
    #queries和attention_weights的形状为(查询个数, 键-值 对个数)
    queries = queries.repeat_interleave(keys.shape[1]).reshape((-1, keys.shape[1]))
    self.attention_weights = nn.functional.softmax(
      -((queries - keys) * self.w) ** 2 / 2, dim=1   #dim=1表示按行计算
    )
    return torch.bmm(
      self.attention_weights.unsqueeze(1),
      values.unsqueeze(-1)
    ).reshape(-1)  #并将结果变成一维

net = NWKernelRegression()
loss = nn.MSELoss(reduction='none')
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
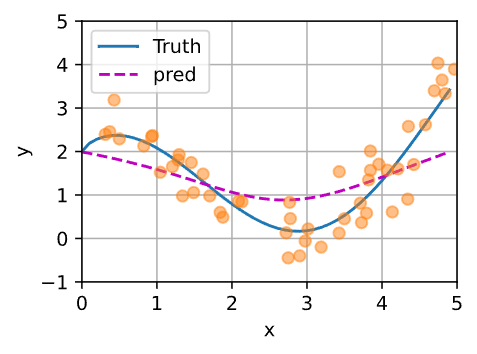
animator = d2l.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])

for epoch in range(5):
  # keys的形状:(n_test，n_train)，每一行包含着相同的训练输入（例如，相同的键）
  keys = x_train.repeat((n_test, 1))
  # value的形状:(n_test，n_train)
  values = y_train.repeat((n_test, 1))
  y_hat = net(x_test, keys, values).unsqueeze(1).detach()
  
  optimizer.zero_grad()  #梯度清零
  l = loss(net(x_train, keys, values), y_train)  #计算损失
  l.sum().backward()  #将损失之和进行反向传播
  optimizer.step()  #更新
  print(f'epoch {epoch + 1}, loss {float(l.sum()):.6f}')
  animator.add(epoch + 1, float(l.sum()))

plt.show()
plot_kernel_reg(y_hat)

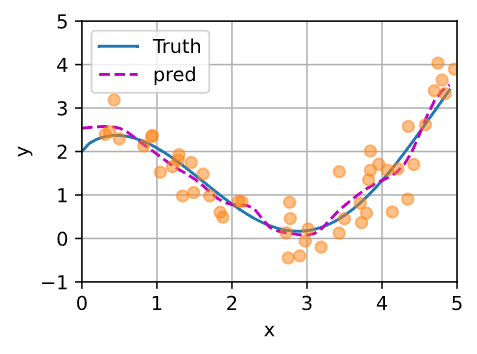
image-20220802055910798

得到的曲线不如之前的平滑，但是更加接近真实值

image-20220802060021336